Chapter 22 Bayesian data analysis
22.1 Learning goals
- Doing Bayesian inference “by hand”
- Understanding the effect that prior, likelihood, and sample size have on the posterior.
- Doing Bayesian data analysis with
greta- A simple linear regression.
22.2 Load packages and set plotting theme
library("knitr") # for knitting RMarkdown
library("janitor") # for cleaning column names
library("patchwork") # for figure panels
library("tidybayes") # tidying up results from Bayesian models
library("greta") # for writing Bayesian models
library("gganimate") # for animations
library("extraDistr") # additional probability distributions
library("broom") # for tidy regression results
library("tidyverse") # for wrangling, plotting, etc. theme_set(theme_classic() + #set the theme
theme(text = element_text(size = 20))) #set the default text size
opts_chunk$set(comment = "",
fig.show = "hold")22.3 Doing Bayesian inference “by hand”
22.3.1 Sequential updating based on the Beta distribution
# data
data = c(0, 1, 1, 0, 1, 1, 1, 1)
# whether observation is a success or failure
success = c(0, cumsum(data))
failure = c(0, cumsum(1 - data))
# I've added 0 at the beginning to show the prior
# plotting function
fun.plot_beta = function(success, failure){
ggplot(data = tibble(x = c(0, 1)),
mapping = aes(x = x)) +
stat_function(fun = "dbeta",
args = list(shape1 = success + 1, shape2 = failure + 1),
geom = "area",
color = "black",
fill = "lightblue") +
coord_cartesian(expand = F) +
scale_x_continuous(breaks = seq(0.25, 0.75, 0.25)) +
theme(axis.title = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
plot.margin = margin(r = 1, t = 0.5, unit = "cm"))
}
# generate the plots
plots = map2(success, failure, ~ fun.plot_beta(.x, .y))
# make a grid of plots
wrap_plots(plots, ncol = 3)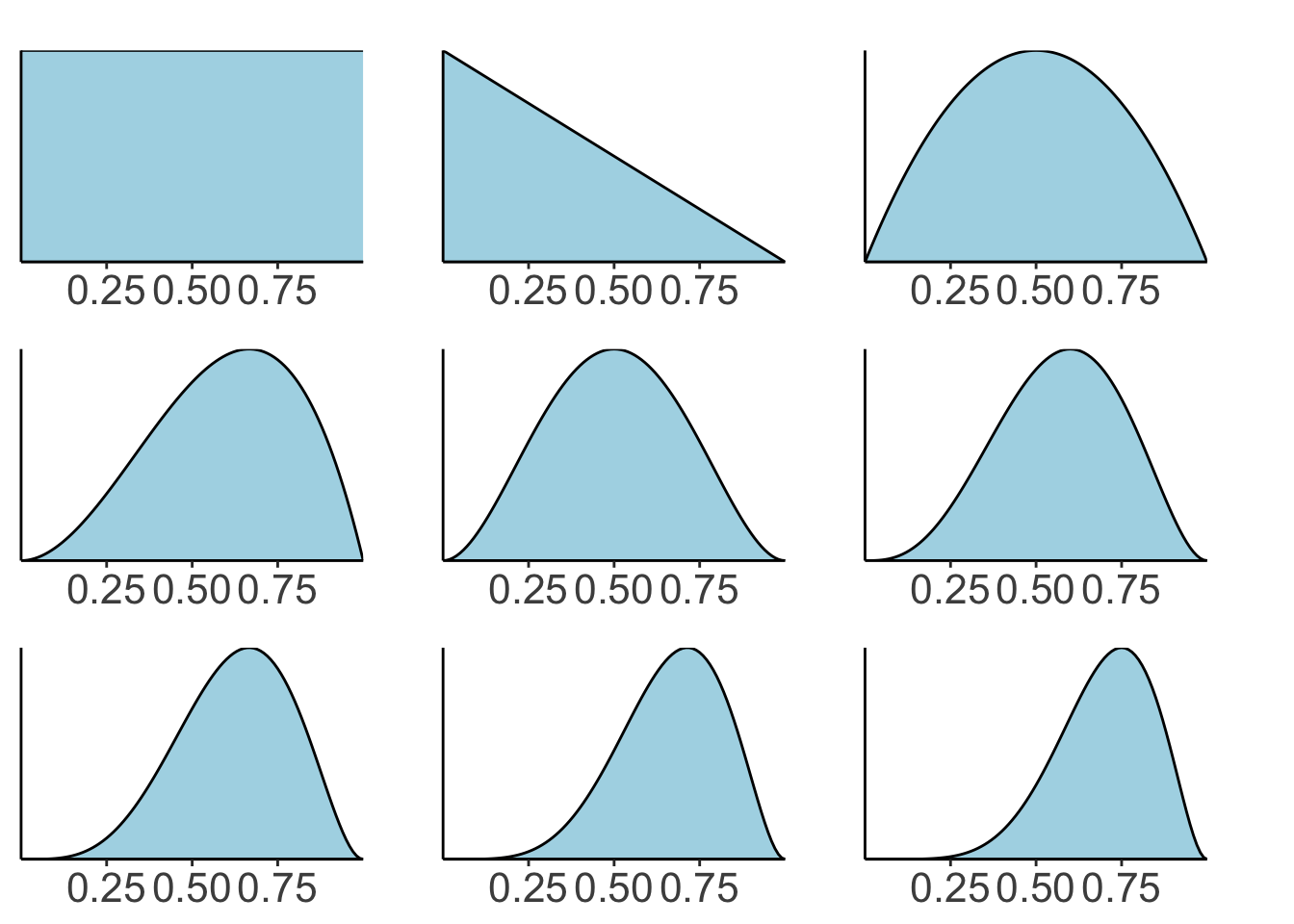
22.3.2 Coin flip example
Is the coin biased?
# data
data = rep(0:1, c(8, 2))
# parameters
theta = c(0.1, 0.5, 0.9)
# prior
prior = c(0.25, 0.5, 0.25)
# prior = c(0.1, 0.1, 0.8) # alternative setting of the prior
# prior = c(0.000001, 0.000001, 0.999998) # another prior setting
# likelihood
likelihood = dbinom(sum(data == 1), size = length(data), prob = theta)
# posterior
posterior = likelihood * prior / sum(likelihood * prior)
# store in data frame
df.coins = tibble(theta = theta,
prior = prior,
likelihood = likelihood,
posterior = posterior) Visualize the results:
df.coins %>%
pivot_longer(cols = -theta,
names_to = "index",
values_to = "value") %>%
mutate(index = factor(index, levels = c("prior", "likelihood", "posterior")),
theta = factor(theta, labels = c("p = 0.1", "p = 0.5", "p = 0.9"))) %>%
ggplot(data = .,
mapping = aes(x = theta,
y = value,
fill = index)) +
geom_bar(stat = "identity",
color = "black") +
facet_grid(rows = vars(index),
switch = "y",
scales = "free") +
annotate("segment", x = -Inf, xend = Inf, y = -Inf, yend = -Inf) +
annotate("segment", x = -Inf, xend = -Inf, y = -Inf, yend = Inf) +
theme(legend.position = "none",
strip.background = element_blank(),
axis.title.y = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
axis.title.x = element_blank(),
axis.line = element_blank())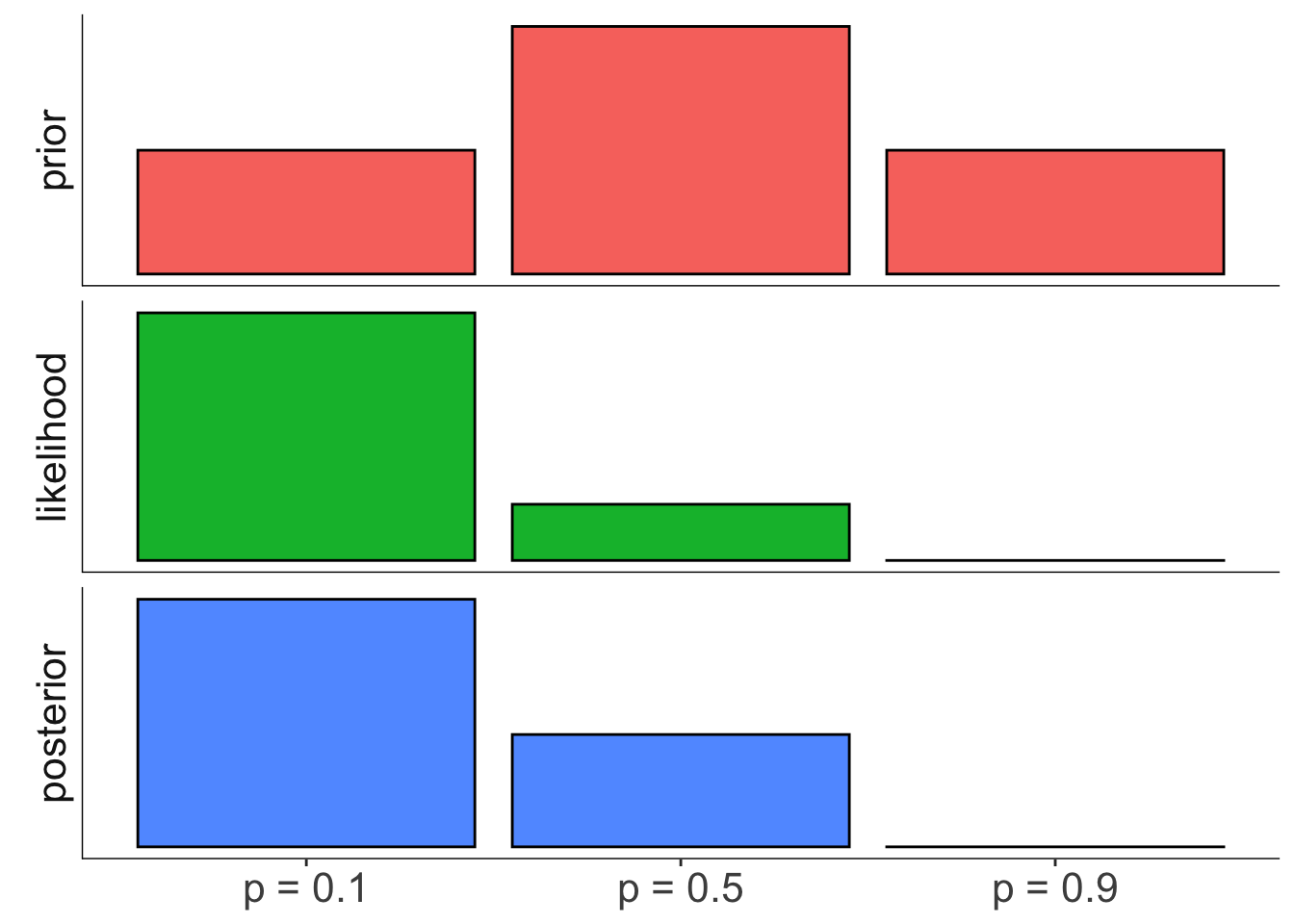
22.3.3 Bayesian inference by discretization
22.3.3.1 Effect of the prior
# grid
theta = seq(0, 1, 0.01)
# data
data = rep(0:1, c(8, 2))
# calculate posterior
df.prior_effect = tibble(theta = theta,
prior_uniform = dbeta(theta, shape1 = 1, shape2 = 1),
prior_normal = dbeta(theta, shape1 = 5, shape2 = 5),
prior_biased = dbeta(theta, shape1 = 8, shape2 = 2)) %>%
pivot_longer(cols = -theta,
names_to = "prior_index",
values_to = "prior") %>%
mutate(likelihood = dbinom(sum(data == 1),
size = length(data),
prob = theta)) %>%
group_by(prior_index) %>%
mutate(posterior = likelihood * prior / sum(likelihood * prior)) %>%
ungroup() %>%
pivot_longer(cols = -c(theta, prior_index),
names_to = "index",
values_to = "value")
# make the plot
df.prior_effect %>%
mutate(index = factor(index, levels = c("prior", "likelihood", "posterior")),
prior_index = factor(prior_index,
levels = c("prior_uniform", "prior_normal", "prior_biased"),
labels = c("uniform", "symmetric", "asymmetric"))) %>%
ggplot(data = .,
mapping = aes(x = theta,
y = value,
color = index)) +
geom_line(size = 1) +
facet_grid(cols = vars(prior_index),
rows = vars(index),
scales = "free",
switch = "y") +
scale_x_continuous(breaks = seq(0, 1, 0.2)) +
annotate("segment", x = -Inf, xend = Inf, y = -Inf, yend = -Inf) +
annotate("segment", x = -Inf, xend = -Inf, y = -Inf, yend = Inf) +
theme(legend.position = "none",
strip.background = element_blank(),
axis.title.y = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
axis.text.x = element_text(size = 10),
axis.line = element_blank())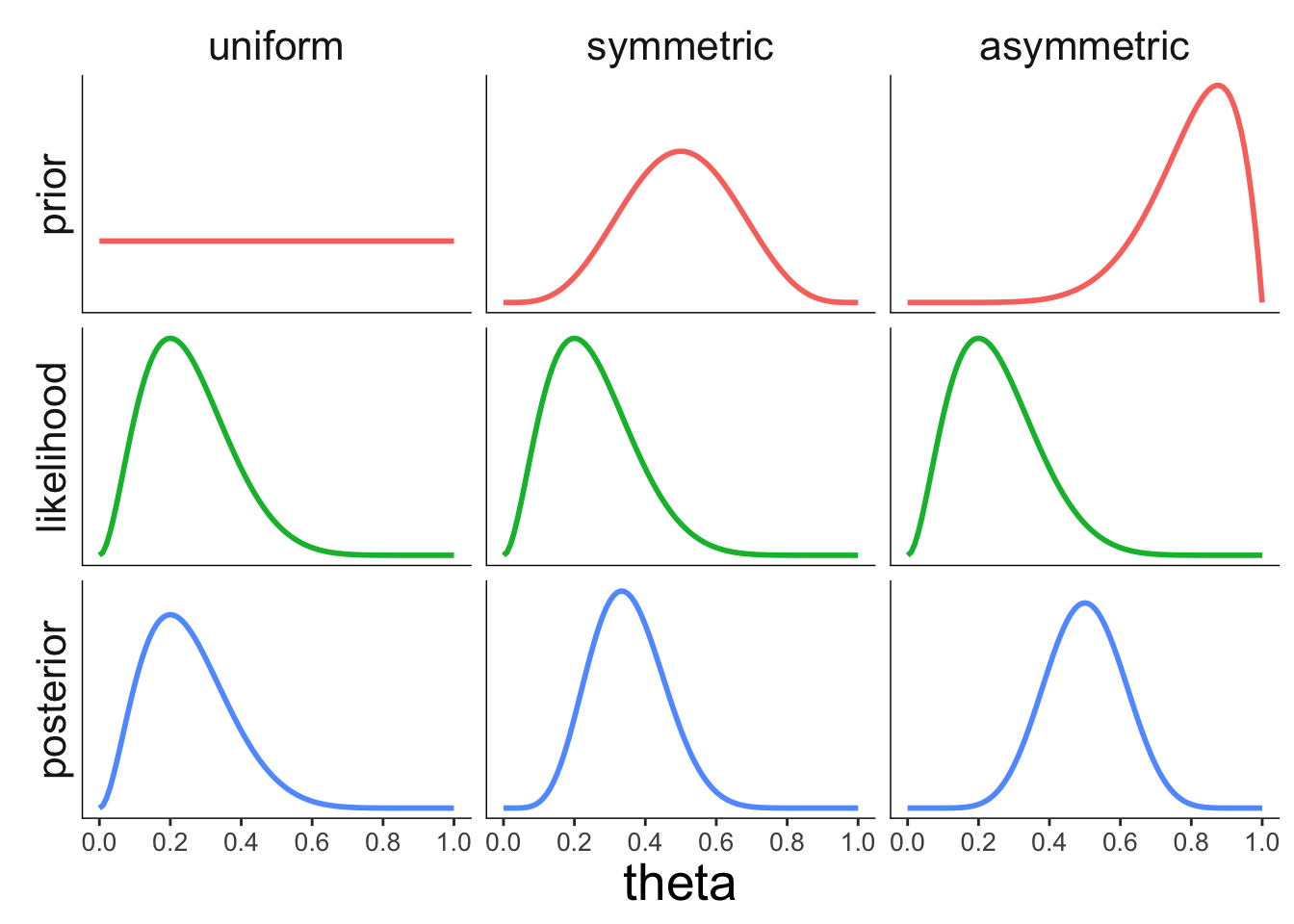
Figure 2.6: Illustration of how the prior affects the posterior.
22.3.3.2 Effect of the likelihood
# grid
theta = seq(0, 1, 0.01)
df.likelihood_effect = tibble(theta = theta,
prior = dbeta(theta, shape1 = 2, shape2 = 8),
likelihood_left = dbeta(theta, shape1 = 1, shape2 = 9),
likelihood_center = dbeta(theta, shape1 = 5, shape2 = 5),
likelihood_right = dbeta(theta, shape1 = 9, shape2 = 1)) %>%
pivot_longer(cols = -c(theta, prior),
names_to = "likelihood_index",
values_to = "likelihood") %>%
group_by(likelihood_index) %>%
mutate(posterior = likelihood * prior / sum(likelihood * prior)) %>%
ungroup() %>%
pivot_longer(cols = -c(theta, likelihood_index),
names_to = "index",
values_to = "value")
df.likelihood_effect %>%
mutate(index = factor(index, levels = c("prior", "likelihood", "posterior")),
likelihood_index = factor(likelihood_index,
levels = c("likelihood_left",
"likelihood_center",
"likelihood_right"),
labels = c("left", "center", "right"))) %>%
ggplot(data = .,
mapping = aes(x = theta,
y = value,
color = index)) +
geom_line(size = 1) +
facet_grid(cols = vars(likelihood_index),
rows = vars(index),
scales = "free",
switch = "y") +
scale_x_continuous(breaks = seq(0, 1, 0.2)) +
annotate("segment", x = -Inf, xend = Inf, y = -Inf, yend = -Inf) +
annotate("segment", x = -Inf, xend = -Inf, y = -Inf, yend = Inf) +
theme(legend.position = "none",
strip.background = element_blank(),
axis.title.y = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
axis.text.x = element_text(size = 10),
axis.line = element_blank(),
strip.text.x = element_blank())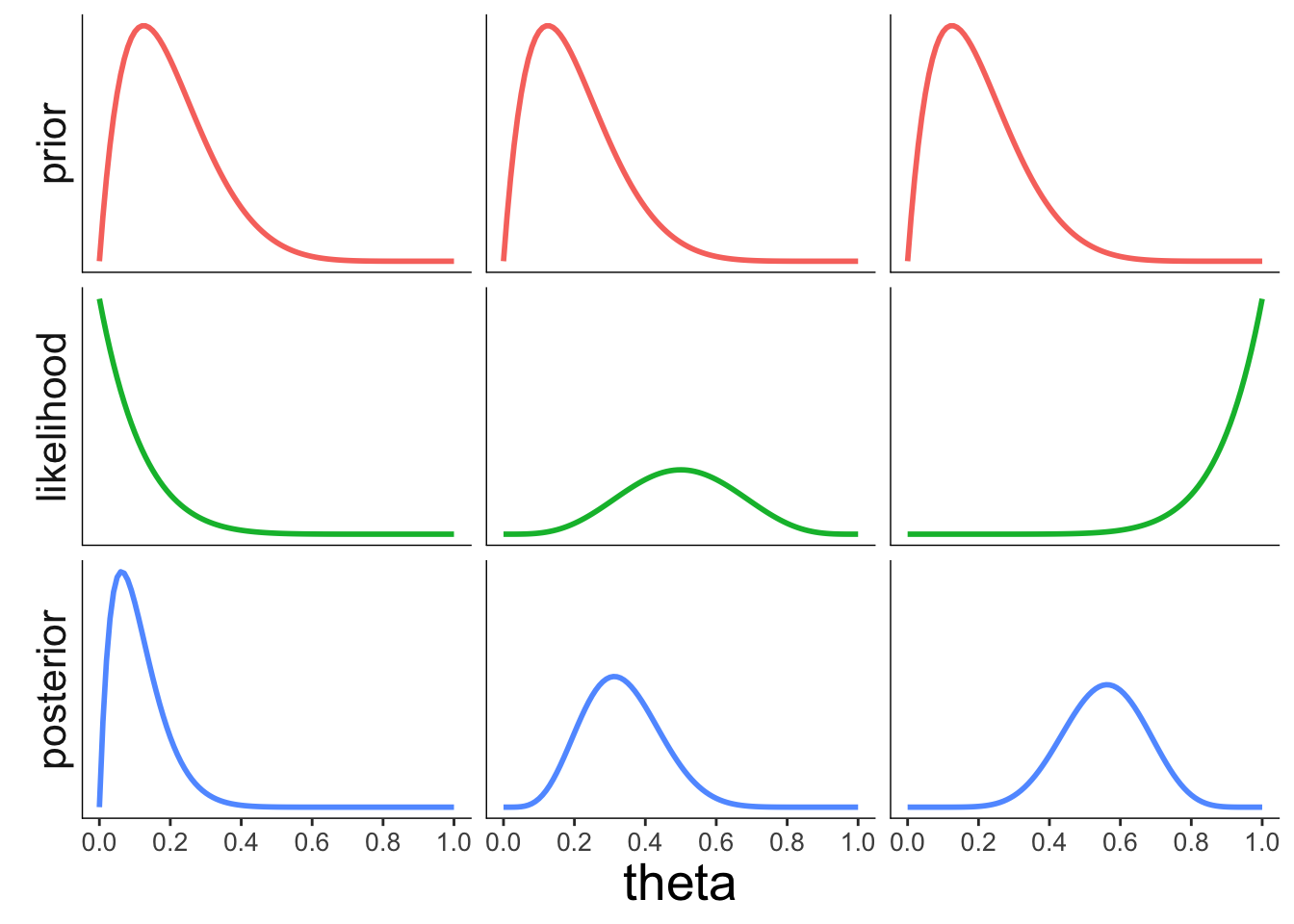
Figure 2.7: Illustration of how the likelihood of the data affects the posterior.
22.3.3.3 Effect of the sample size
# grid
theta = seq(0, 1, 0.01)
df.sample_size_effect = tibble(theta = theta,
prior = dbeta(theta, shape1 = 5, shape2 = 5),
likelihood_low = dbeta(theta, shape1 = 2, shape2 = 8),
likelihood_medium = dbeta(theta,
shape1 = 10,
shape2 = 40),
likelihood_high = dbeta(theta,
shape1 = 20,
shape2 = 80)) %>%
pivot_longer(cols = -c(theta, prior),
names_to = "likelihood_index",
values_to = "likelihood") %>%
group_by(likelihood_index) %>%
mutate(posterior = likelihood * prior / sum(likelihood * prior)) %>%
ungroup() %>%
pivot_longer(cols = -c(theta, likelihood_index),
names_to = "index",
values_to = "value")
df.sample_size_effect %>%
mutate(index = factor(index, levels = c("prior", "likelihood", "posterior")),
likelihood_index = factor(likelihood_index,
levels = c("likelihood_low",
"likelihood_medium",
"likelihood_high"),
labels = c("n = low", "n = medium", "n = high"))) %>%
ggplot(data = .,
mapping = aes(x = theta,
y = value,
color = index)) +
geom_line(size = 1) +
facet_grid(cols = vars(likelihood_index),
rows = vars(index),
scales = "free",
switch = "y") +
scale_x_continuous(breaks = seq(0, 1, 0.2)) +
annotate("segment", x = -Inf, xend = Inf, y = -Inf, yend = -Inf) +
annotate("segment", x = -Inf, xend = -Inf, y = -Inf, yend = Inf) +
theme(legend.position = "none",
strip.background = element_blank(),
axis.title.y = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
axis.text.x = element_text(size = 10),
axis.line = element_blank())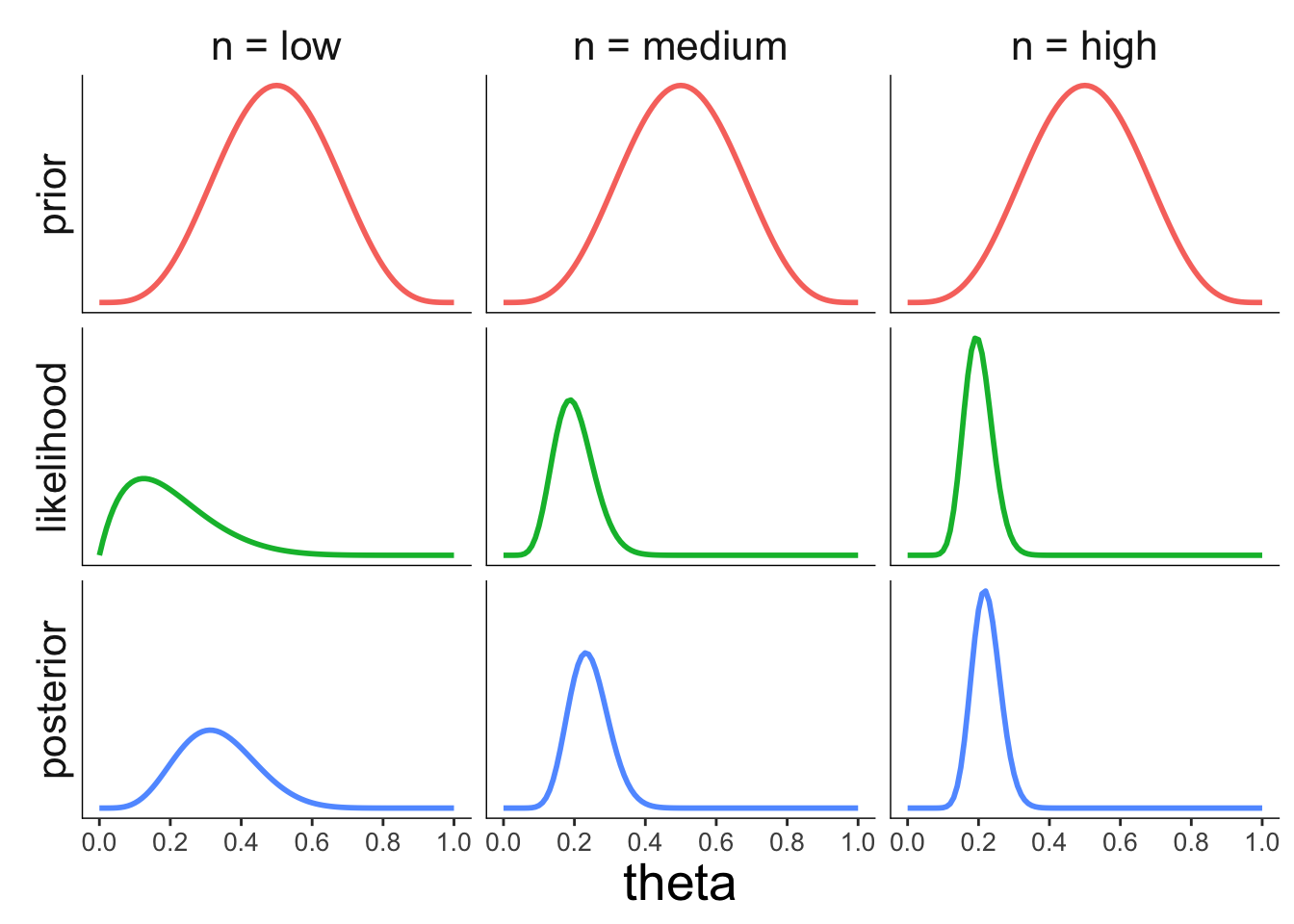
22.4 Doing Bayesian inference with Greta
You can find out more about how get started with “greta” here: https://greta-stats.org/articles/get_started.html. Make sure to install the development version of “greta” (as shown in the “install-packages” code chunk above: devtools::install_github("greta-dev/greta")).
22.4.1 Attitude data set
# load the attitude data set
df.attitude = attitudeVisualize relationship between how well complaints are handled and the overall rating of an employee
ggplot(data = df.attitude,
mapping = aes(x = complaints,
y = rating)) +
geom_point()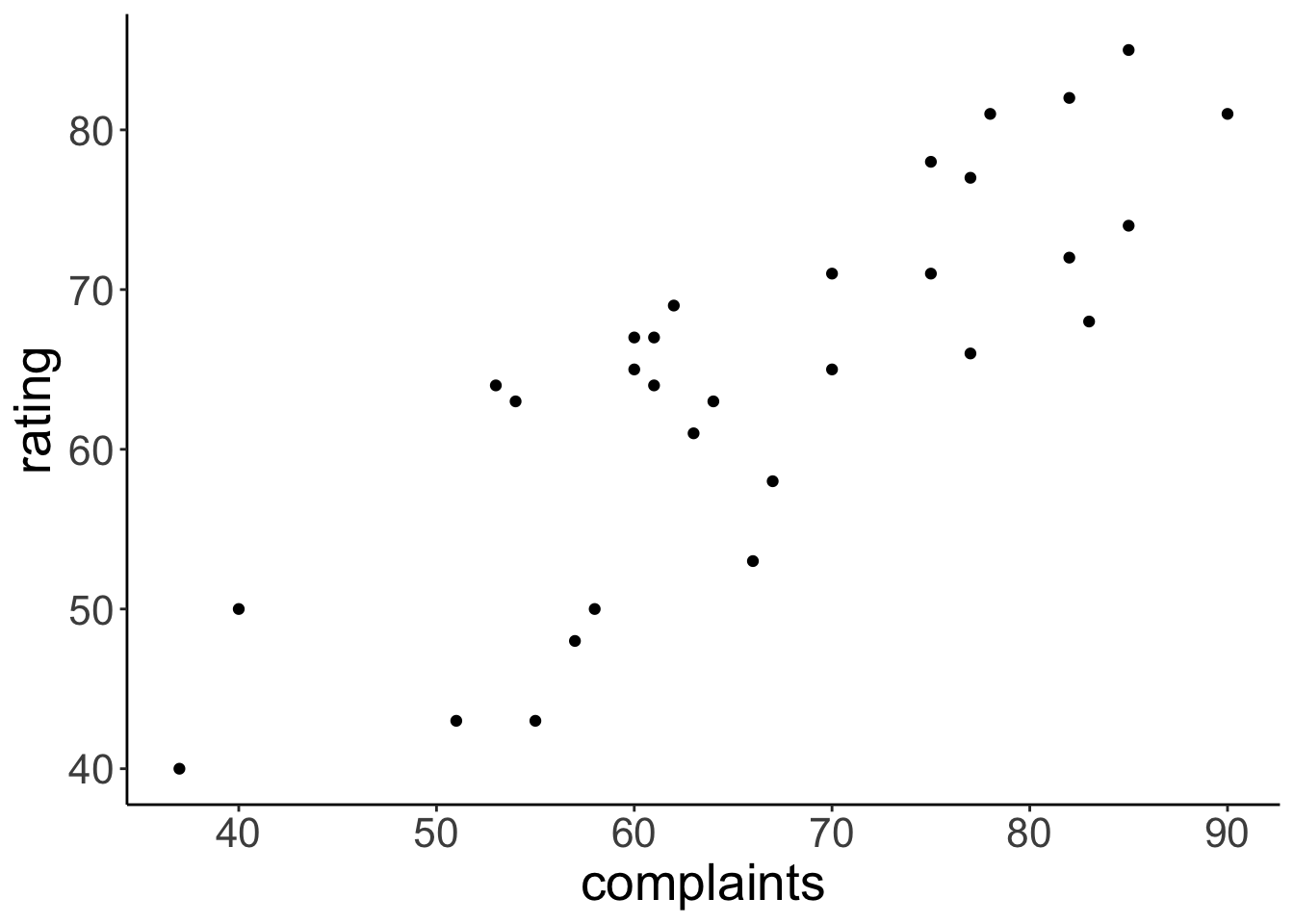
22.4.2 Frequentist analysis
# fit model
fit.lm = lm(formula = rating ~ 1 + complaints,
data = df.attitude)
# print summary
fit.lm %>%
summary()
Call:
lm(formula = rating ~ 1 + complaints, data = df.attitude)
Residuals:
Min 1Q Median 3Q Max
-12.8799 -5.9905 0.1783 6.2978 9.6294
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.37632 6.61999 2.172 0.0385 *
complaints 0.75461 0.09753 7.737 1.99e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.993 on 28 degrees of freedom
Multiple R-squared: 0.6813, Adjusted R-squared: 0.6699
F-statistic: 59.86 on 1 and 28 DF, p-value: 1.988e-08Visualize the model’s predictions
ggplot(data = df.attitude,
mapping = aes(x = complaints,
y = rating)) +
geom_smooth(method = "lm",
formula = "y ~ x",
color = "black") +
geom_point()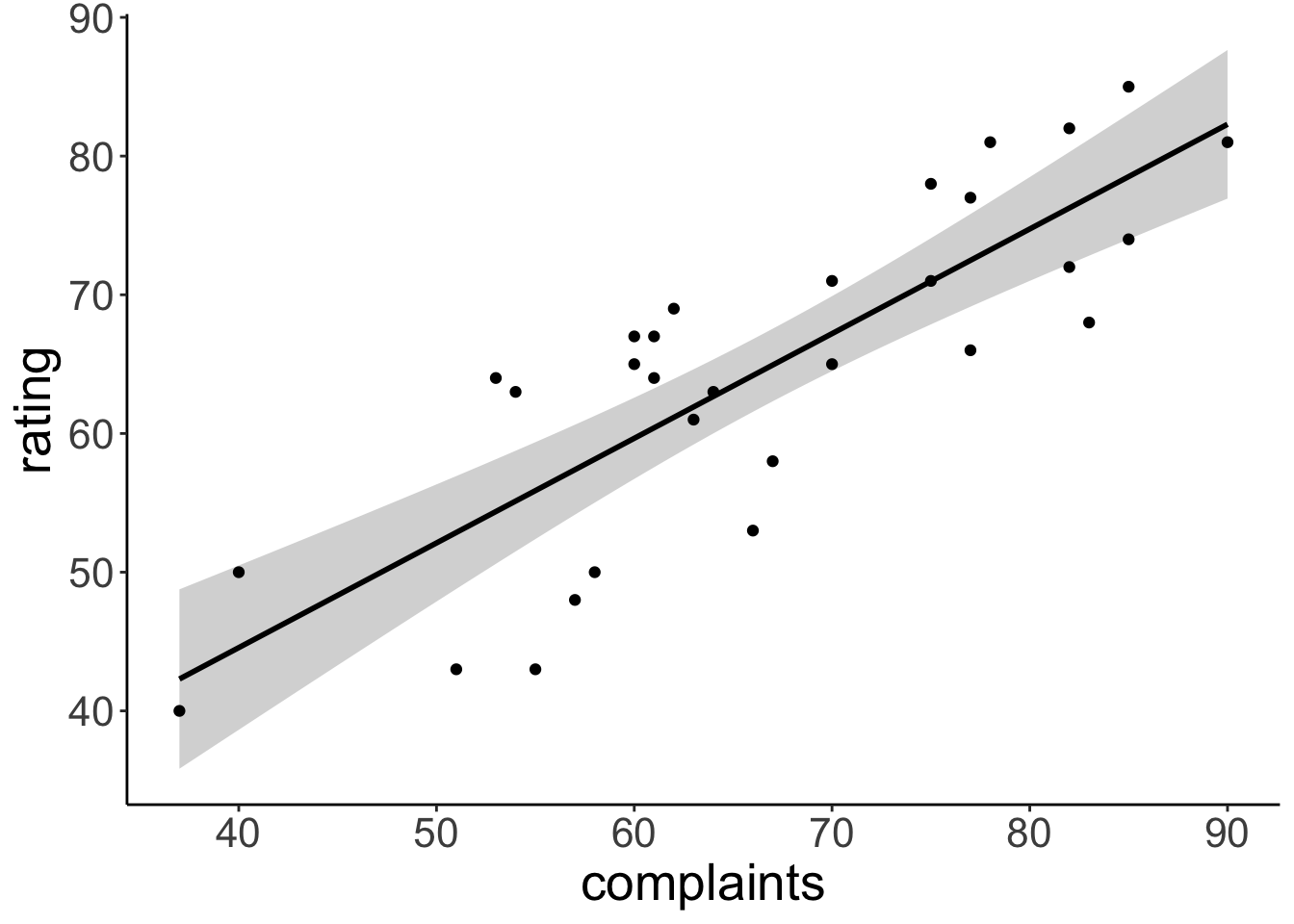
22.4.3 Bayesian regression
22.4.3.1 Fit the model
set.seed(1)
# variables & priors
b0 = normal(0, 10)
ℹ Initialising python and checking dependencies, this may take a moment.[K
✔ Initialising python and checking dependencies ... done
22.4.3.3 Visualize the posteriors
This is what the posterior looks like for the three parameters in the model:
df.draws %>%
select(draw:sd) %>%
pivot_longer(cols = -draw,
names_to = "index",
values_to = "value") %>%
ggplot(data = .,
mapping = aes(x = value)) +
stat_density(geom = "line") +
facet_grid(rows = vars(index),
scales = "free_y",
switch = "y") +
annotate("segment", x = -Inf, xend = Inf, y = -Inf, yend = -Inf) +
annotate("segment", x = -Inf, xend = -Inf, y = -Inf, yend = Inf) +
theme(legend.position = "none",
strip.background = element_blank(),
axis.title.y = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
axis.text.x = element_text(size = 10),
axis.line = element_blank(),
strip.text.x = element_blank())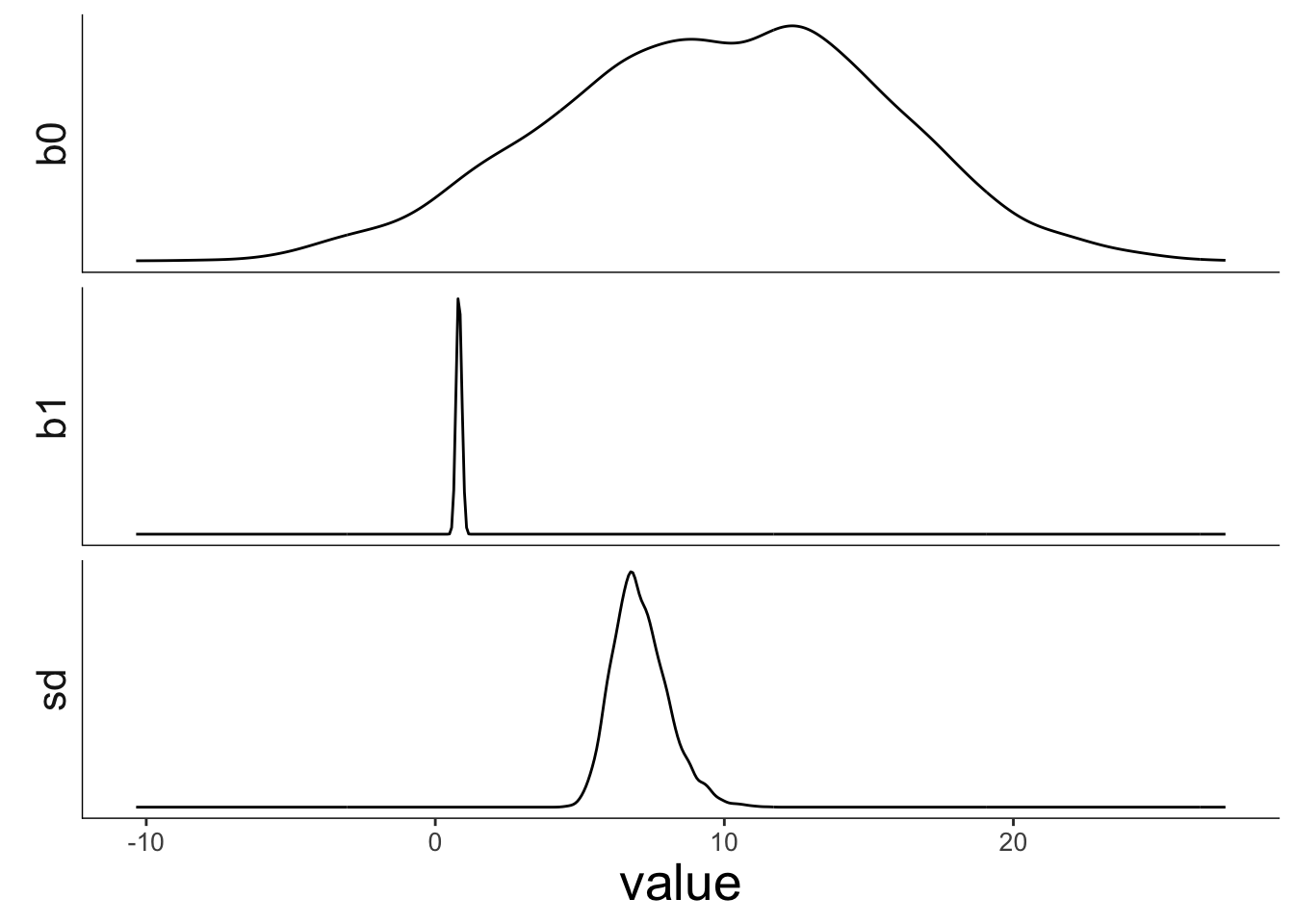
#### Credible interval vs. confidence interval
fit.lm %>%
tidy(conf.int = T) %>%
ggplot(mapping = aes(y = term,
x = estimate,
xmin = conf.low,
xmax = conf.high)) +
geom_pointrange()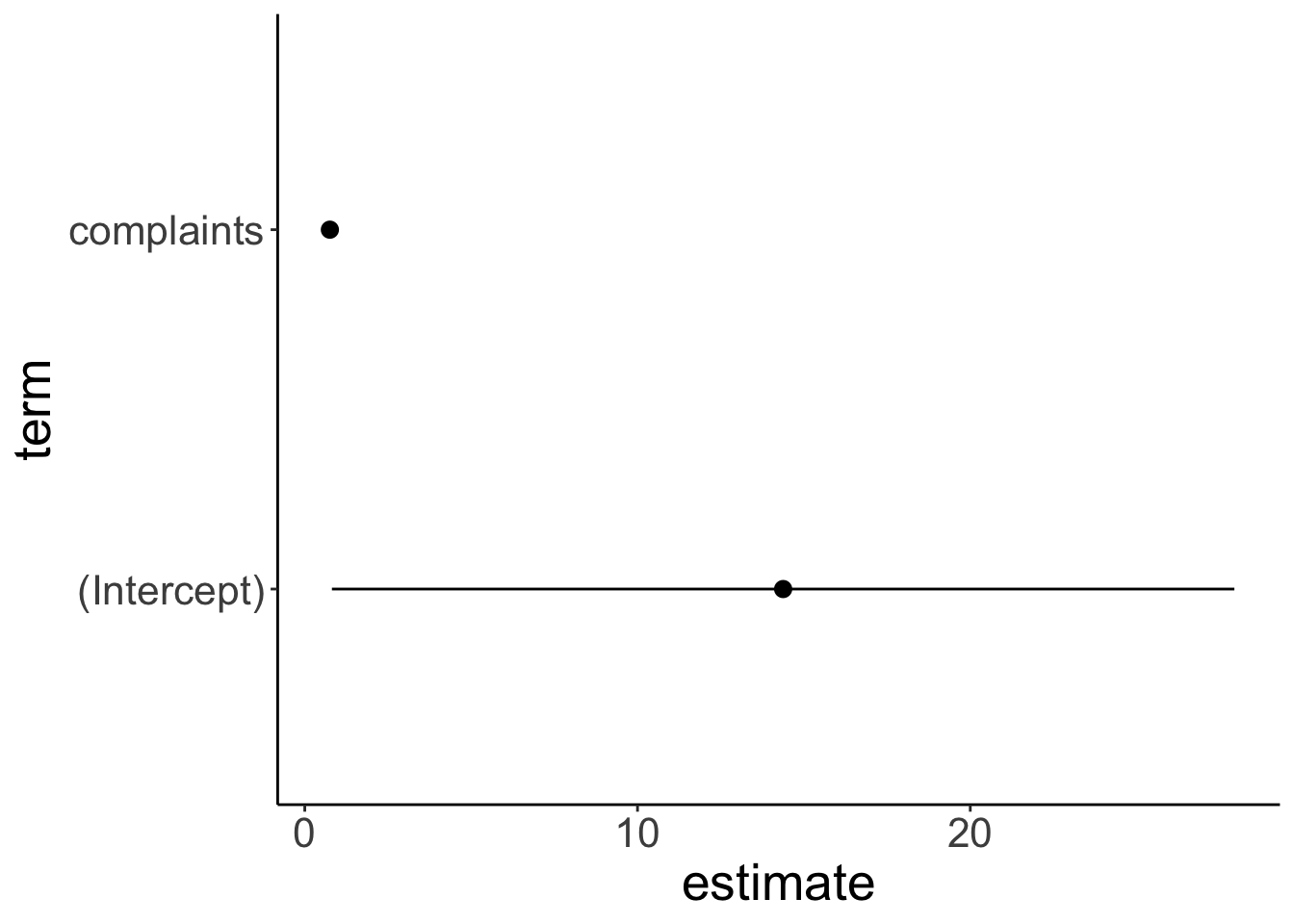
22.4.3.4 Visualize model predictions
Let’s take some samples from the posterior to visualize the model predictions:
ggplot(data = df.attitude,
mapping = aes(x = complaints,
y = rating)) +
geom_abline(data = df.draws %>%
slice_sample(n = 50),
mapping = aes(intercept = b0,
slope = b1),
alpha = 0.3,
color = "lightblue") +
geom_point()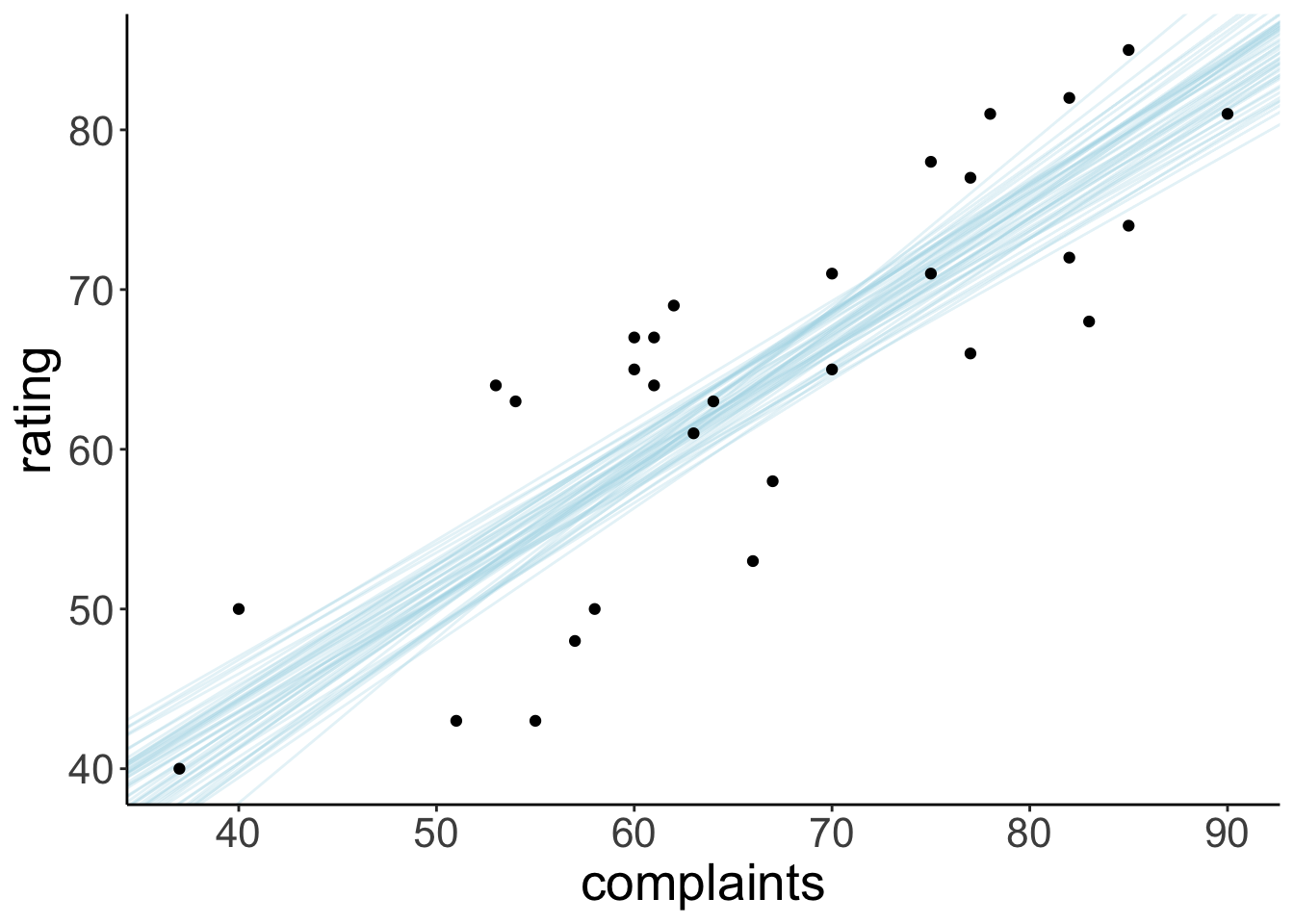 
22.4.3.5 Posterior predictive check
Let’s make an animation that illustrates what predicted data sets (based on samples from the posterior) would look like:
p = df.draws %>%
slice_sample(n = 10) %>%
mutate(complaints = list(seq(min(df.attitude$complaints),
max(df.attitude$complaints),
length.out = nrow(df.attitude)))) %>%
unnest(c(complaints)) %>%
mutate(prediction = b0 + b1 * complaints + rnorm(n(), sd = sd)) %>%
ggplot(aes(x = complaints, y = prediction)) +
geom_point(alpha = 0.8,
color = "lightblue") +
geom_point(data = df.attitude,
aes(y = rating,
x = complaints)) +
coord_cartesian(xlim = c(20, 100),
ylim = c(20, 100)) +
transition_manual(draw)
animate(p,
nframes = 60,
width = 800,
height = 600,
res = 96,
type = "cairo")
# anim_save("posterior_predictive.gif")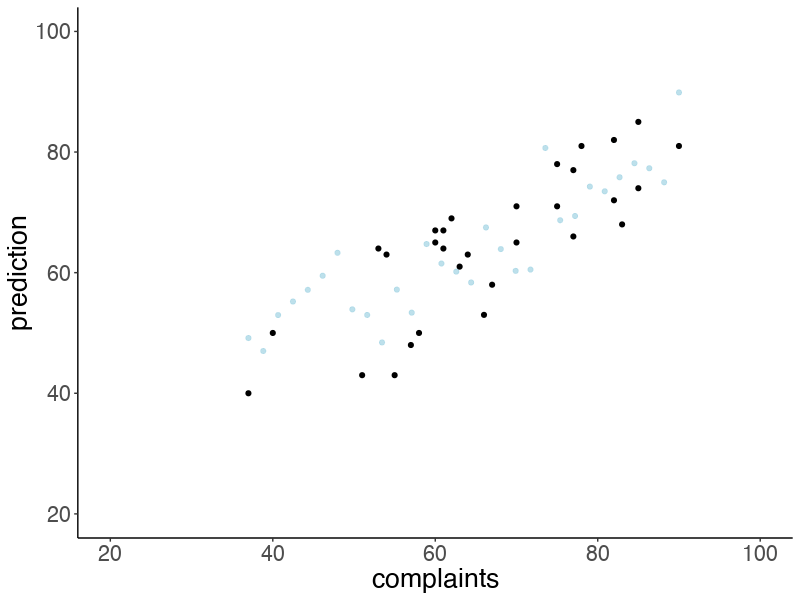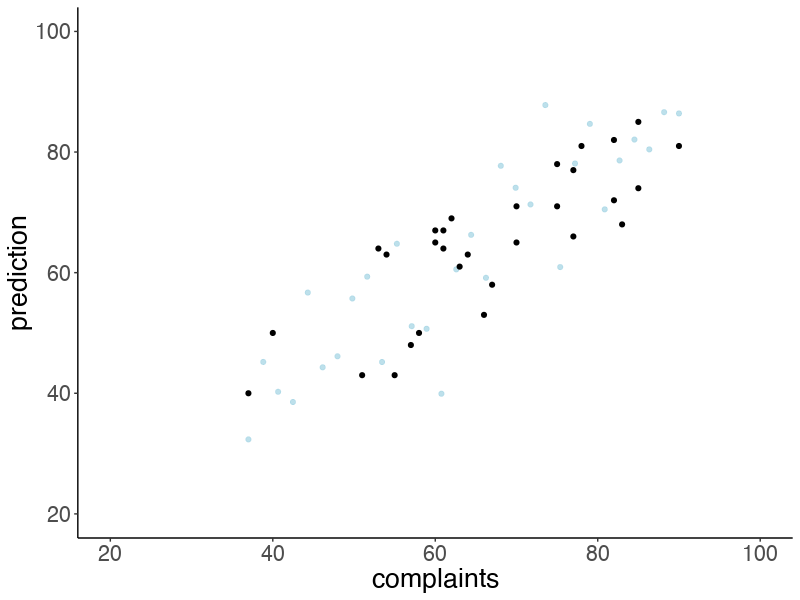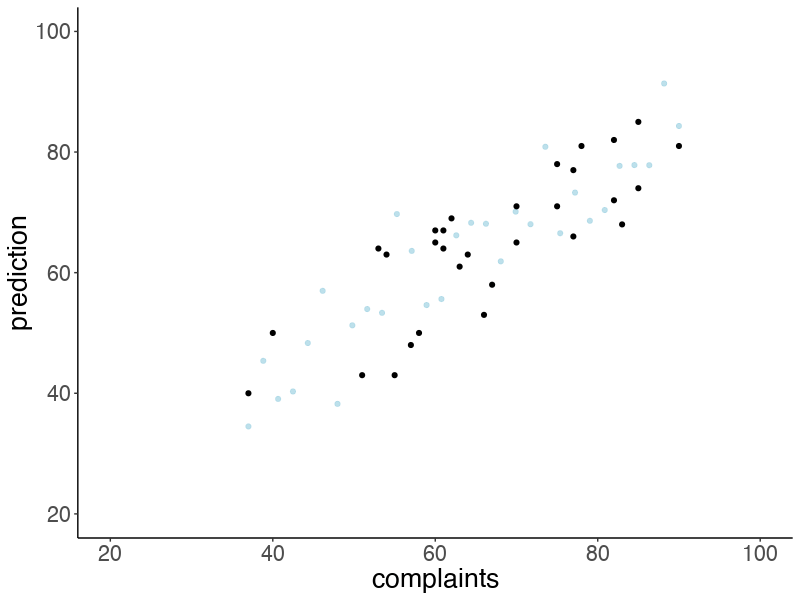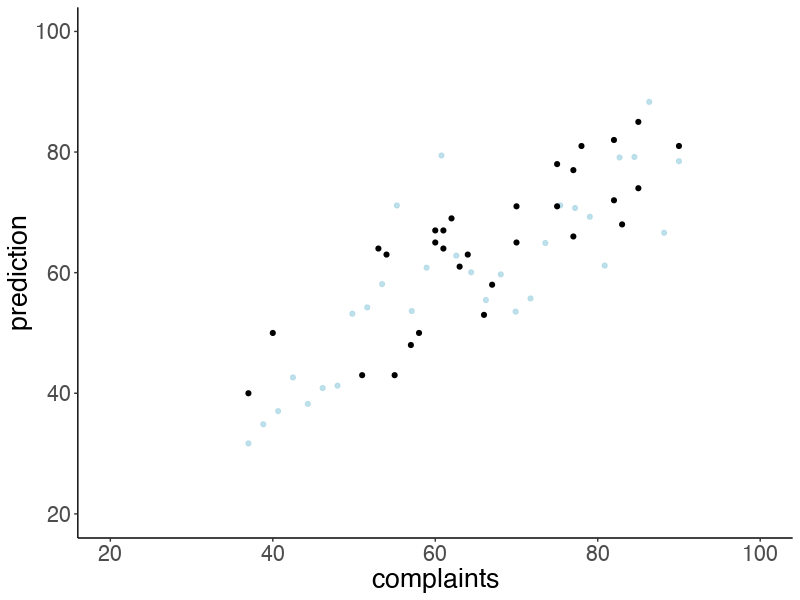
22.4.3.6 Prior predictive check
And let’s illustrate what data we would have expected to see just based on the information that we encoded in our priors.
sample_size = 10
p = tibble(b0 = rnorm(sample_size, mean = 0, sd = 10),
b1 = rnorm(sample_size, mean = 0, sd = 10),
sd = rhcauchy(sample_size, sigma = 3),
draw = 1:sample_size) %>%
mutate(complaints = list(runif(nrow(df.attitude),
min = min(df.attitude$complaints),
max = max(df.attitude$complaints)))) %>%
unnest(c(complaints)) %>%
mutate(prediction = b0 + b1 * complaints + rnorm(n(), sd = sd)) %>%
ggplot(aes(x = complaints, y = prediction)) +
geom_point(alpha = 0.8,
color = "lightblue") +
geom_point(data = df.attitude,
aes(y = rating,
x = complaints)) +
transition_manual(draw)
animate(p,
nframes = 60,
width = 800,
height = 600,
res = 96,
type = "cairo")
# anim_save("prior_predictive.gif")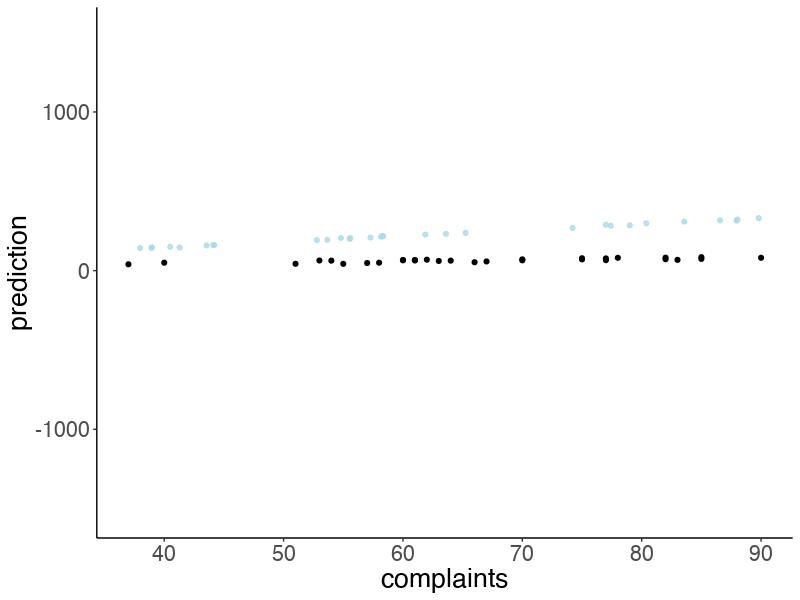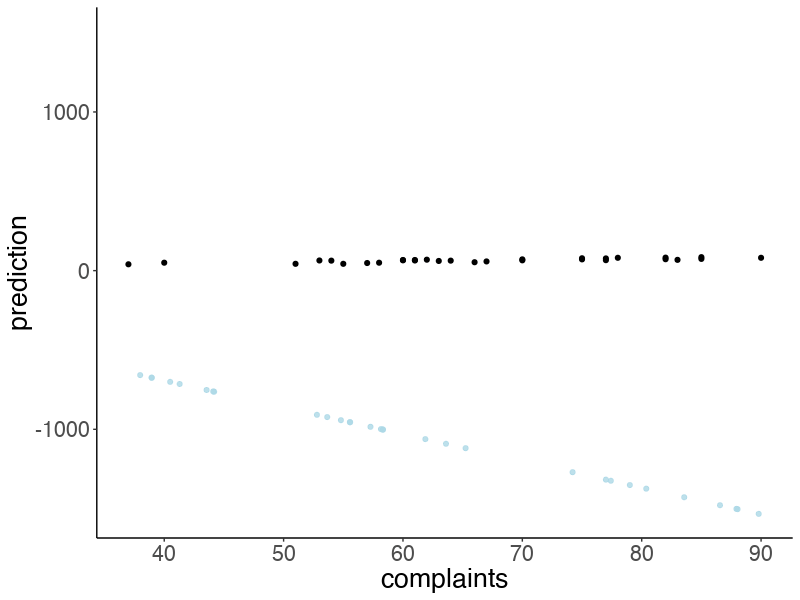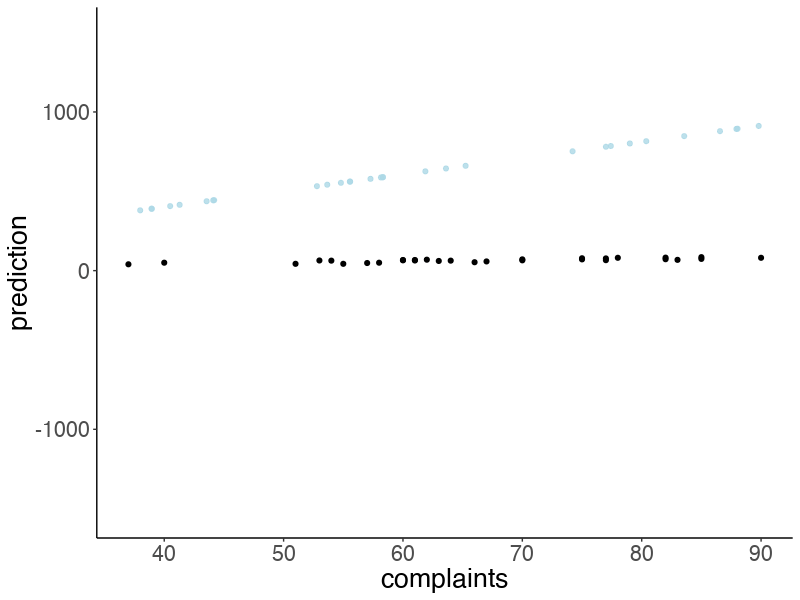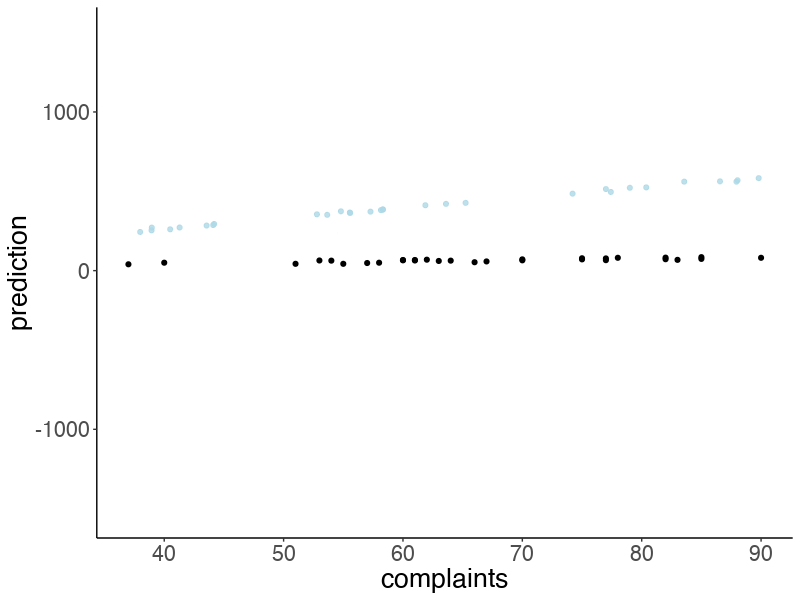
22.5 Session info
Information about this R session including which version of R was used, and what packages were loaded.
sessionInfo()R version 4.1.2 (2021-11-01)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] forcats_0.5.1 stringr_1.4.0 dplyr_1.0.9 purrr_0.3.4
[5] readr_2.1.2 tidyr_1.2.0 tibble_3.1.7 tidyverse_1.3.1
[9] broom_0.8.0 extraDistr_1.9.1 gganimate_1.0.7 ggplot2_3.3.6
[13] greta_0.4.2 tidybayes_3.0.2 patchwork_1.1.1 janitor_2.1.0
[17] knitr_1.39
loaded via a namespace (and not attached):
[1] nlme_3.1-157 fs_1.5.2 lubridate_1.8.0
[4] RColorBrewer_1.1-3 progress_1.2.2 httr_1.4.3
[7] rprojroot_2.0.3 tensorA_0.36.2 DiagrammeRsvg_0.1
[10] tools_4.1.2 backports_1.4.1 bslib_0.3.1
[13] utf8_1.2.2 R6_2.5.1 mgcv_1.8-40
[16] DBI_1.1.2 colorspace_2.0-3 ggdist_3.1.1
[19] withr_2.5.0 tidyselect_1.1.2 prettyunits_1.1.1
[22] processx_3.5.3 curl_4.3.2 compiler_4.1.2
[25] rvest_1.0.2 cli_3.3.0 arrayhelpers_1.1-0
[28] xml2_1.3.3 labeling_0.4.2 bookdown_0.26
[31] posterior_1.2.1 sass_0.4.1 scales_1.2.0
[34] checkmate_2.1.0 callr_3.7.0 tfruns_1.5.0
[37] digest_0.6.29 rmarkdown_2.14 base64enc_0.1-3
[40] pkgconfig_2.0.3 htmltools_0.5.2 parallelly_1.31.1
[43] highr_0.9 dbplyr_2.1.1 fastmap_1.1.0
[46] htmlwidgets_1.5.4 rlang_1.0.2 readxl_1.4.0
[49] rstudioapi_0.13 visNetwork_2.1.0 jquerylib_0.1.4
[52] farver_2.1.0 generics_0.1.2 svUnit_1.0.6
[55] jsonlite_1.8.0 tensorflow_2.8.0 distributional_0.3.0
[58] magrittr_2.0.3 Matrix_1.4-1 Rcpp_1.0.8.3
[61] munsell_0.5.0 fansi_1.0.3 abind_1.4-5
[64] reticulate_1.24 lifecycle_1.0.1 stringi_1.7.6
[67] whisker_0.4 yaml_2.3.5 snakecase_0.11.0
[70] plyr_1.8.7 grid_4.1.2 parallel_4.1.2
[73] listenv_0.8.0 crayon_1.5.1 lattice_0.20-45
[76] splines_4.1.2 haven_2.5.0 hms_1.1.1
[79] ps_1.7.0 pillar_1.7.0 igraph_1.3.1
[82] codetools_0.2-18 reprex_2.0.1 glue_1.6.2
[85] evaluate_0.15 V8_4.1.0 gifski_1.6.6-1
[88] modelr_0.1.8 png_0.1-7 vctrs_0.4.1
[91] tzdb_0.3.0 tweenr_1.0.2 cellranger_1.1.0
[94] gtable_0.3.0 future_1.25.0 assertthat_0.2.1
[97] xfun_0.30 coda_0.19-4 DiagrammeR_1.0.9
[100] globals_0.14.0 ellipsis_0.3.2 here_1.0.1